nathan_H
Hierarchical Clustering 본문
Hierarchical Clustering
Hierarchical Clustering은 뜻 그대로
계층 군집화로 비슷한 군집끼리 묶어 가면서 최종 적으로는
하나의 케이스가 될때까지 군집을 묶는 클러스터링 알고리즘이다.
(K-means와 다르게 미리 군집 개수를 정하는 것이 아니라
학습을 하면서 스스로 군집 개수를 정한다.)

알고리즘 진행은 다음과 같다
1) 각 데이터들을 cluster라고 가정
2) 각 데이터 pair 사이의 distance 계산
3) 가장 distance가 작은 pair를 하나의 cluster로 묶음
4) 모든 데이터가 하나의 cluster로 묶이지 않으면2)반복
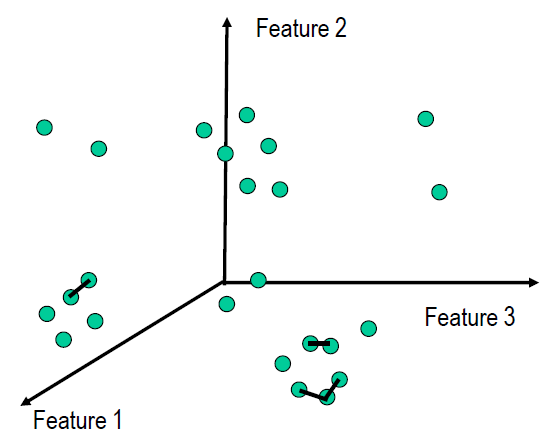

예시 참고 자료 - http://www.datamarket.kr/xe/board_mXVL91/9807
데이터분석 - 8.군집분석[H-cluster]
군집분석[H-cluster]부분을 맡게된 인하대학교 통계학과 12학번 투빅스 3기 박희경입니다. 앞글 군집분석[K-means]에서 전체적인 군집분석의 개념에 대루었기 때문에, H-cluster와 군집분석의 진단에 대해서 알아보겠습니다. 틀린 내용이나 부족한 내용이 있으면 지적해주시고 수정하겠습니다. H-cluster는 Hierarchical Clustering(계층적 군집분석)의 줄임말입니다. K-means에서는 군집들끼리 서로 배타적으로 겹치는 부분이
www.datamarket.kr
Hierarchical Clustering 변형(variants)
두개의 cluster 간에distance 를 잴때,
어떤 방식으로 distance를 재느냐에 따라 여러가지 변형 존재한다.



위에 그림 처럼 보통 distance을 잴때 formal하게
1. single-link: minimum distance of all pairs of patterns from two clusters
2. complete-link: maximum distance
3. average-link : average distance
이렇게 총 3가지 방식을 사용한다.
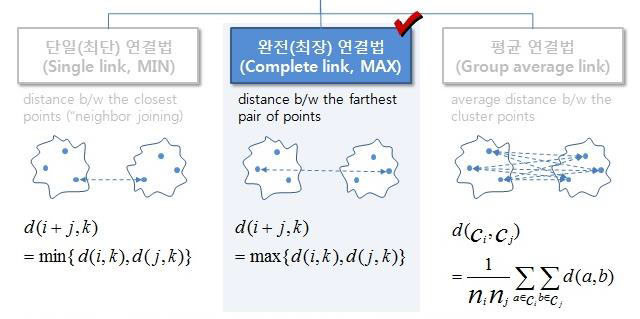

위 예시는 avergae link으로
연결한 예시이다.
Clustering 을 위한 Distance Metric
여태 예제들은 distance 그냥 주어진 상태라고
가정을 했지만, 실제로는 두 데이터간의
distance 값을 계산해야 하는 경우가 대부분이다.
그리고 두 데이터간에 어떤 방식으로 distance 재느냐,
즉 어떤 distance metric을 사용하느냐가
군집결과가 달라지기 때문에 매우 중요하다.
단적인 예로
‘흰색냉장고’ vs ‘흰색지우개‘ 의distance 를 구한다고 가정
- 색깔로만 distance 구할경우: distance 는거의 0
-크기로distance 구할 경우: distance 가 매우 큼(예: 200cm vs. 3cm)
Distance / Similarity Metric
Similarity의 반대: Dissimilarity (distance)
Distance / Similarity Metric에는
- Euclidean distance
- Cosine similarity
- KL divergence
- Mahalanobis distance
- Hamming distance
와 같은 다양한 기법들이 있는데
그중 많이 쓰이는 Euclidean distance 에 대해 알아보자.
Euclidean distance

수식

적용 예시)
Data
X1: 180cm, 90kg, short-hair
X2: 175cm, 88kg, short-hair
X3: 162cm, 52kg, long-hair
X4: 155cm, 58kg, long-hair

특징

여기서 한 층 더 나아가
1) Short-hair와 같은 categorical feature,
혹은 누락된 feature들에 대해 어떻게 해야 할까?
2) (3.0, 223, red) 와 같이 여러 타입의 feature들이 섞여 있는
경우의 유사도 계산은 어떻게 해야 할까?
3) 데이터가 특이한 경우인 예를 들어
몸무게는 50~100kg인데 키가 10cm인 경우에 문제는
무엇이고 해결방법은 무엇인가?
Feature scaling
그것은 바로 Feature 값들의 scaling을 통해 해결 할 수 있다.
Normalization : 0~1 사이로 변환
Standardization : Normal 분포에 의해 변환


Missing value 처리.
Missing feature value 다루는 일반적인 방법으로는
Missing value 원인은 기계고장, 천재지변, 사망, 거부 등으로 다양하다.
그래서 모델에 따라 다루는 방법은 각기 다르지만,
일반적으로는 아래와 같이 할 수 있다.
(distance 값이0~1 사이라고가정)
Categorical (nominal) feature
-> 두개의 데이터중 한쪽이라도 missing 이면1
Numerical feature
-> 둘다missing 이면1
-> 한쪽만missing 이면, ‘상대쪽 평균치’를 취하거나,
‘1 –상 대쪽 평균치’
Entropy & KL Divergence & Mutual Information
Euclidean distance이외 에도 다양한 방법들이 있는데
그 가운데 Entropy & KL Divergence & Mutual Information을 살펴보자.
Entropy
- Discrete case

- Continuous case
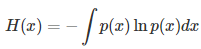
로 두가지 case로 나뉘어 사용된다.
Kullback-Leibler divergence
Kullback-Leibler divergence은
두개의 distribution 간의 차이를
measure (같으면0, 다를수록커짐)방법이다.

그리고 KL Divergence는
NOT symmetric인 특성을 가지고 있다.

KL-divergence 참고 블로그
- https://reniew.github.io/17/
Mutual Information
Mutual Information은
두개의 random variable 들이
얼마나 ‘의존‘적인지 measure하는 방법이다.

Entropy 와의 관계

참고 : Random Variable
[ Random Variable ]
-확률변수
-표본공간S의표본점w에실수값을대응(실험, 샘플링으로생기는값)


Hierarchical Clustering 특징.
장점.
1) Dendrogram provides a visual inspection
2) Most widely used due to ease of use and visualization
3) K-means와 달리 사전에 군집수 k를 설정할 필요가 없습니다.
단점
1)Computationally prohibitive: O (n2)
2) Can not repair the faults from previous steps
그 외 특징들
1) Distance 잴때, Average-link 방식이
가장 성능이 좋은편이었다는 연구결과가 있다.
2) 거의 대부분의 군집화 알고리즘들이 겪는 문제인데,
‘적절한 군집개수‘ 결정,‘ 적절한 군집인지 판단‘ 등을 어떻게 하느냐가 중요
3) Distance function 을 뭐를 쓰느냐에 따라 결과가 완전 바뀜

'Big Data > ML' 카테고리의 다른 글
| Gaussian Mixture Model - GMM (0) | 2019.06.06 |
|---|---|
| EM Algorithms (0) | 2019.06.06 |
| Ensembles (0) | 2019.06.04 |
| Marginalize (0) | 2019.06.01 |
| KNN Algorithms ( 최근접 이웃 알고리즘) (0) | 2019.05.31 |




