Support Vector Machine .

 본내용은 순천향대학교 정영섭 교수님과

관련 블로그를 참조한 글입니다.

 

블로그 list

 

-https://ratsgo.github.io/machine%20learning/2017/05/23/SVM/

- https://wikidocs.net/5719

 

 

 

 

Support Vector Machine

 

 

출처 - https://ratsgo.github.io/machine%20learning/2017/05/23/SVM/

 

 

B1, B2선중에 머가 더 두개의 labe을 잘 나눈 선이라고 생각하는가??

 

아마 대부분 B1이라고 말을 할것이다.

 

이것이 SVM에 Motivation이자 

SVM을 가장 잘 설명하는 내용이다.

 

 

즉 SVM는 데이터 클래스를 분류하는 목적으로

어떻게 하면 클래스를 잘 나누어줄수 있을까라는 생각에서

시작이 된거라고 볼수 있고

데이터 클래스를 가장 잘나누어주는

decision boundary를 구하는 과정이다.

 

 

Support Vector, Max margin

 

 

출처 - http://www.alliedacademies.org/articles/decision-support-system-based-on-the-support-vector-machines-and-the-adaptive-support-vector-machines-algorithm-for-solving-chest-10050.html

 

SVM은 Support Vector와 Max-Margin을 활용을

decision boundary을 구하게 된다.

 

 

 

1) Max Margin

 

위 그림에서 볼 수 있듯이 클래스를 가장 나눠주기 위해선

각 클래스의 거리가 최대인 지점을 찾아주면 된다.

이것을 Max-margin이라고 하며

Max-margin은 유일해야한다.

 

 

2) Support Vector

 

Max-margin을 구하기 위해선 각 클래스를 

경계 지어주는 선들이 필요한데 

이것을 Support vector라고 하면

 

 

 

출처 - https://imgur.com/afe8W3S

즉 Decision Boundary는 Max-margin을 가지는

Support vector의 중간선이 되는 것이다.

 

위 그림에서 볼 수 있듯이 Binary Support Vector에서 

decision boundary 수식은

wtx + b = 0이 된다.

 

 

 

SVM 분류 방법.

 

SVM은 Decision boundary에 데이터를 적용한 '부호'로 판별을 해

분류를 진행을 하게 된다.

 

 Binary 기준에서 임의의 데이터를 decision boundary 수식에 적용하면.

w*u(임의의 데이터) + b < 0 일 경우'-'클래스로 분류하고 

w*u(임의의 데이터) + b > 0 일 경우 '+'클래스로 분류한다.

 

즉 이 작업은 u(임의의 데이터)를 w에 projection 하고난 후

그 길이가 boundary에 닿느냐, 안닿느냐를 보고 결정하는 것이다.

 

좀 더 formal하게 정리해보면, boundary와

노란색 선까지의 거리를 1이라고 가정하면

 

w *x(-) + b <= -1

w * x(+) + b >= 1

이렇게 표현할 수 있다.

 

(잘 분류낼 수 있는 svm을 얻기 위해서는 데이터를 기반으로

충분한 학습과정을 거쳐 w와 b를 계산해야한다.)

 

 

SVM 수식.

 

 

 

 decision boundary는

앞서 계속 이야기 했듯이

'다른 클래스 간의 거리를 최대화'한다는

조건을 추가해 수식을 표현해 보자.

 

 

i번째 데이터의 label yi 정의

->

 

 

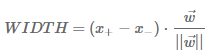
위에 식 대입

즉 max margin 구하는 것은 

w라는 weight matrix에 대한 '최적화(최소화)'문제가 된다.

 

 

 

Lagrange multiplier

 

Lagrange Multiplier 자세한 설명 참고 

- https://untitledtblog.tistory.com/96

라그랑주 승수법 (Lagrange Multiplier Method)

 

위에서 봤듯이 svm의 목적은 Max margin을

가진 경계면을 구하는 것이고

이것을 구하기 위해선 weight matrix을 최소화 해줘야 한다.

 

 

그리고 추가로 SVM은 Support Vector을 기준으로 분류되야 하기 때문에

Support vector만 고려한다는 제약조건을 넣은 상태에서

W을 최소화 하기 위해 Lagrange Multiplier방법을 사용한다.

 

계산상의 편의를 위해 위에 식처럼 변해도 본질은 바뀌지 않는다.

(미분 가능하게 만듬)

 

 

 

수식

 

 

 

KKT 조건에서는 Lp를 미지수로

각각 편미분한 식이 0이 되는 지점에서 최소값을 갖는다.

 

 

위에 식에서 지금까지 도출한 결과를 토대로

Lp를 정리하면 아래와 같다.

 

즉 식을 변환하는 과정에서  α에 관한 식으로 간단해졌다.

 

α의 최고차항의 계수가 음수이므로 최소값을 찾는 문제가

최대값을 찾는 문제로 바뀌었다. 

 

 

이 문제는 Quadratic programming 이라는 알고리즘으로 풀 수 있으며,
quadratic은 convex 모양을 가지므로, 

현재 상태에서의 ‘최적‘해를 찾을 수 있음을 의미이기도 하다.

(global optimal) (성능이 높게 나온다)

 우선 위 ‘최대화 수식’을 통해 𝛼 를 찾음
위에 식을 기반으로 w 찾음
위에 식을 기반으로 b 찾음

 

 

KKT condition.

KKT condition은 Lagrange Multiplier 방법 적용 시, 

부등식 제약조건에 대해 적용가능하도록 

바꿔주는 용도인데,

 

svm에 적용될 때에는 이것이 

support vector만 고려하도록 해주는 역활을 수행한다.

 

 

 

 

 

비선형 패턴을 위한 SVM

 

 

Slack Variable

 

Slack Variable은

Decision boundary 양 옆의 경계선 내에 들어왔거나 일부 틀린
데이터들에 대하여 대충 넘어가주기 위한 변수이다.

 

slack variable을 추가함으로 인해 원래의 최적화 

문제는 풀기라 어려워 진다는 점이 있다.

 

여기서 변수 C: 오분류되었지만 대충 넘어가주는 것에 대한 비용이고,

 C를 크게 할수록 대충 넘어가기 어려워지므로, 정확히
분류해내도록 학습 (overfitting 유도) 하고
C를 작게 할수록 대충 넘어가기 쉬워지므로, 정확하지 않게
분류해내도록 학습하게 된다.

 

 

Kernel trick

Kernel trick은

선형 판별이 안 되는 경우에 대하여, 선형 판별 되는 공간으로 변경한
것처럼 kernel 함수를 통과시켜 연산 수행한다.

 

 

source - https://www.researchgate.net/figure/Kernel-trick_fig12_325856401

 

수식

 

 

 

 

SVM의 해

 

svm에서 구하고자 하는 분류 경계면은 wTx+b이다. 

w와 b를 찾으면 SVM의 해를 구할 수 있는 것이다.

 

KKT 조건을 탐색하는 과정에서 w는 다음과 같이 도출되었고

 

x, y는 가지고 있는 학습데이터이므로 라그랑지안 승수인

α값들만 알면 w를 찾을 수 있다.

 

그런데 여기에서 αi가 0인 관측치들은 분류경계면

형성에 아무런 영향을 끼치지 못다.

바꿔 말해 i번째 관측치에 대응하는 라그랑지안 승수 

αi가 0보다 커야 마진 결정에 유의미하다는 것이다.

 

또한 KKT 조건에 의해 함수가 최적값을 가진다면

 

1) αi

2)  yi(wTxi+b−1)

 

둘중 하나는 반드시 0이 되어야 한다.

 

그리고 이 의미는 서포트 벡터만 고려해서

구한다는 의미로 해석할 수 있다.