Linear Regression, Classification

본 글은 순천향대학교 정영섭 교수님 강의 내용과

ratsgo's blog 내용을 토대로 작성 하였습니다.

 

출처 - https://ratsgo.github.io/machine%20learning/2017/07/03/regression/

 

 

 

Linear Regression

 

선형회귀는 수치형 설명변수 x와 연속형 숫자로

이뤄진 종속 변수 y간의 관계를 선형으로 

가정하고 이를 가장 잘 표현할 수 있는

회귀계수를 데이터로 부터 추정하는 모델이다.

 

 

출처 - https://m.blog.naver.com/PostView.nhn?blogId=mykepzzang&logNo=220935571198&proxyReferer=https%3A%2F%2Fwww.google.com%2F

 

 

행렬 X와 종속변수 벡터 Y가 주어졌을 때

다중선형회귀 모델은 다음과 같이 정의된다

 

출처 - https://ratsgo.github.io/machine%20learning/2017/07/03/regression/

 

linear regression의 계수들은 실제값과 모델 예측값의 차이

오차제곱합을 최소로 하는 값들이다.

이를 만족하는 최적의 계수들은 회귀계수에 대해

미분한 식을 0으로 놓고 풀면 아래와 같이 명시적인 해를 구할 수 있다.

다시 말해 우리에게 주어진 X, Y 데이터만

가지고 계수를 단번에 추정할 수 있다.

즉 미분을 통해 최적의 파라메터 β을 구하는 과정인 것이다.

 

참고
y = 실제값
y' = 예측값

Loss = (y - y')2 

Cost = Mean -Squared- Error(MSE)
(실제값과 가설함수의 차이, 데이터 전체에 대한 평균)

 

 

학습 과정

 

1. model 가정

2. paramater 정의

3. parameter 초기값 주기.

4. loss, cost 계산(정의)

5. Gradient decent 적용해 반복적으로

계산을 해 최적의 parameter 찾기.

 

 

 

Gradient Descent 

 

그래프 예시.

출처 - https://hackernoon.com/gradient-descent-aynk-7cbe95a778da

 

 

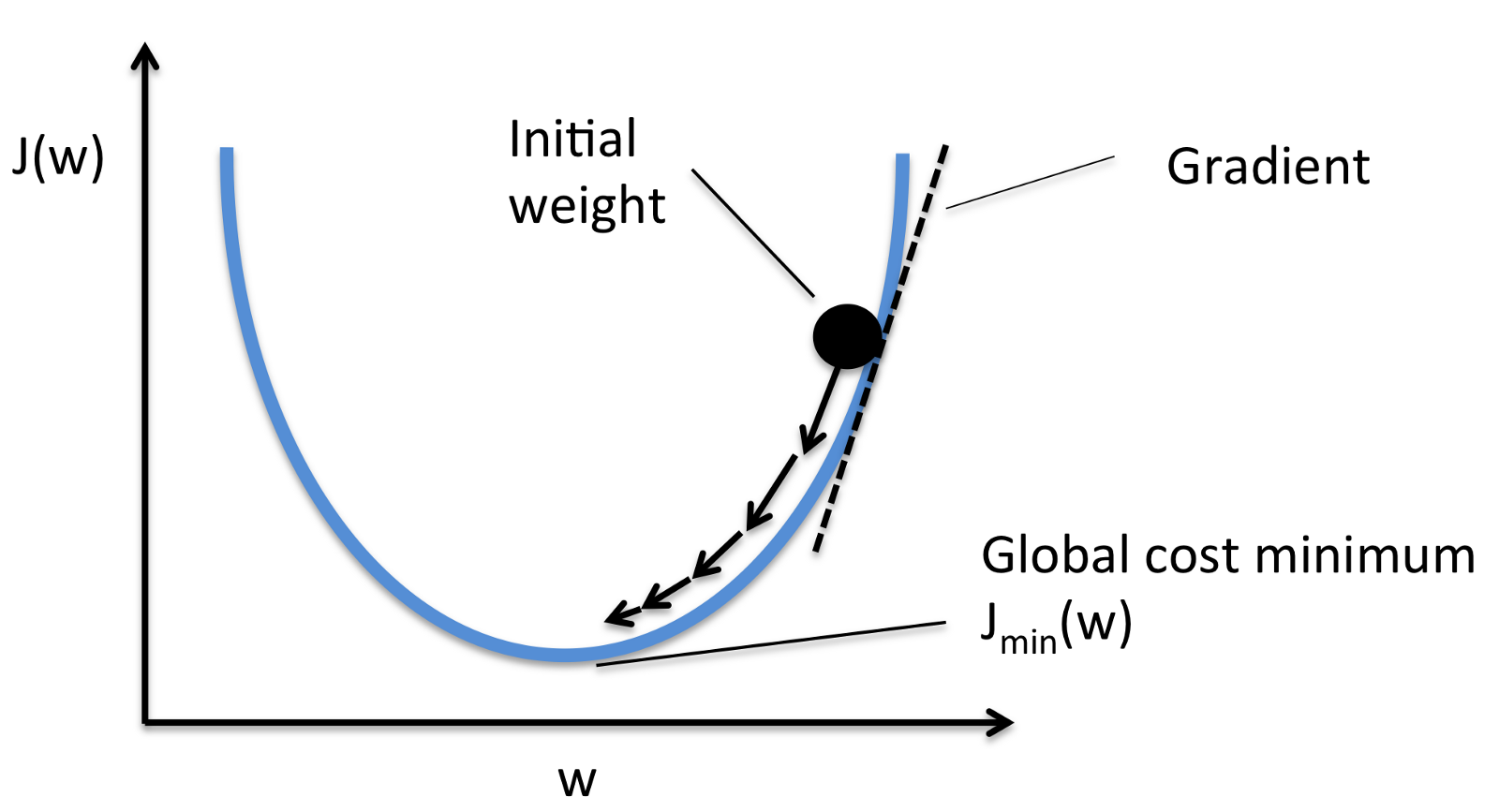
초기 weight(parameter) 값을 주고

 

learning rate(내려오는 정도)을 설정하여

계속해서 학습을 통해

최적의 파라메터를 결정한다.

(learning rate이 너무 낮고 너무 높으면 안된다.)

 

Gradient decent to choose parameter in order to 

minimize cost function

 

 

수식

 

 

결국 미분을 한 후 학습을 통해

최적의 beta(parameter)을 찾는 과정이다.

 

 

Ridge, Lasso Regression

 

 

 

모델을 평가 할 떄 가장 중요한 요소중 하나인

학습 데이터가 

overfitting 되었는지의 유무이다.

 

그래서 linear regression 에서도 

overfitting 이 될수 있기 떄문에

 이를 방지하기 위한 장치로

Ridge, Lasso Regression이 있다.

 

 

 

Ridge, Lasso Regression은 

linear Regression에서 정규화 한것으로

 

Ridge 는 L2 norm으로써 제한하고 

Lasso 는 L1 norm으로 제한하여 적용한다.

*norm -> vector space 상에서 크기 길이를 측정.

 

 

 

 

Ridge regression

 

- 람다가 클수록 ‘제한’이 강해짐

 

 

Lasso regression

 

미분 불가능
- 여러 기법 적용하여 최적화

 

Feature selection 효과 가짐 
> 결과값 생성에 중요하지 않은 것은 과감히weight 값을 0에 가깝게 감소시킴

즉 아래 그림에서 볼수 있듯이 lasso 는 여러점에서 만날 수 있다.

 

 

출처 - https://godongyoung.github.io/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D/2018/02/07/ISL-Linear-Model-Selection-and-Regularization_ch6.html

 

 

 

Logistic Regression(Linear Classification)

 

Logistic Regression은 

선형 회귀 분석으로 분류 문제에 접근 하기 위한 방법이라고 볼 수 있다.

 

 

예시 

- https://bcho.tistory.com/1142

수학포기자를 위한 딥러닝-#4 로지스틱 회귀를 이용한 분류 모델

이항 분류 모델에 대한 예를 들어보자. 종양의 크기에 

따라서 양성 종양(암)인지 음성 종양인지를 판별하는 문제가 있다고 하자.

아래 그림은 종양의 크기에 대한 양성과 음성 여부를 그래프로 나타낸 것인데,

X축은 종양의 크기, Y축은 종양의 양성과 음성 여부를 나타낸다.

1이면 양성 0이면 음성이다.

 

 

 

 

이 경우에는 앞에서 암이 양성인 여부를 판단할때

사용한 y가 0.5라는 기준은 더이상 사용할 수 없게 되고, y가 0.2 일때를,

새 기준으로 잡아서, 암의 양성/음성 여부를 판단해야 한다.

그러면 새로운 데이타가 들어올때 마다 기준점을 다시 잡아야 하는것인가?

또한 그렇게 만든 모델로 예측을 한다면,

학습에 사용되지 않은 큰 데이타가 들어온다면 오류가 발생할 수 도 있다.

그래서, 선형 회귀 분석 모델(Linear regression) 은 이항 분류에 적절하지 않다.

그렇다면 어떤 모델이 적절할까 ?

 

 

이런 문제를 해결 하기 위해 

regression에 적절한 함수로

sigmoid(logistic) 함수를 사용해 

0~1의 확률값을 생성한다.

 

 

 

 

 

 

 

만약, 4개의 점(데이터)에 대하여

,ax + by + c = 0 으로 대입 하게 되면,

4개의점을 모두 지나는‘선‘을 찾게 되고 당연히 못구한다.

 붉은점에 대해서는 f(ax + by + c) 값이 1에 가깝도록,

녹색점에 대해서는f(ax + by + c) 값이 0에 가깝 도록 수식을 정의하여,

‘최적화‘ 문제로풀수있다

> 푼다음엔? 새로운 데이터를 f에 적용하면0~1 사이의값이 나오므로, 

임의의 threshold(임계값) 를기준으로 분류 하면 된다

 

 

 

 

수식

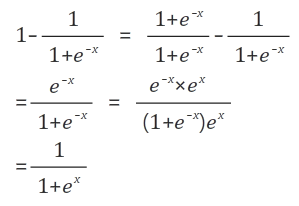
- f를 logistic 을사용: 0~1 값을내어줌
>따라서, f를 확률값 P라고 표기하자

- 붉은점인 경우에는 P의최 대값인 1이 되게 하고,

녹색점인 경우, 1-P가 최대값이 되게 하면 된다.

 

>이러면, 붉은점이든녹색점이든무조건‘최대화’한다는문제로바뀜

 

-붉은점은1, 녹색점은-1로

label을 설정하면, 최대화 문제 수식이 아래와 같다.

 

 

 

파라메터 최적화 

 

>Gradient descent를 사용하여 cost function을

각 파라메터에 대해 편미분 하여

각파라메터를 그 값만큼 업데이트 한다.

 

학습이 끝난Logistic regression 모델을 사용하여 분류하는 수식

모양새를 잘보면, 아래 그림과 같이decision boundary 는linear 하며, 

선형합이 0보다 큰지,작은 지에 의해 결정된다는 것을 알수 있다

 

 

 

지금까지 본 것은binary-case (label두가지)를 위한Logistic regression 이었다.
Label 개수가3개이상이면?

 

 

-> P(Y=3) =1 –P(Y=1) –P(Y=2)

 

 

Classification vs Regression

Classification 은 모델에 의해

예측하려는‘목적값’이 label (discrete value) 범주형

예) 기린vs 하마

-Regression 은 모델에 의해 예측하려는

‘목적값’이real-number (continuous)

예) 아파트평수, 사람의키

- Classification과Regression, 둘다Supervised learning 에속함 

 

-Linear Classification vs Linear Regression
> 둘다‘선형 결합’에 의해 데이터를 모델링
> Linear classification 은0~1 사이의 확률값으로 결과값을 생성 하여,

threshold(경계치) 값을적용함으로써‘분류‘ 문제해결가능

예) 선형합에 대한 threshold 로써0 사용

 

>linear regression 은0~1 바깥의 값들