nathan_H
MLE, MAP 본문
https://ratsgo.github.io/statistics/2017/09/23/MLE/
블로그와 조현제 님의 자료를 정리했음을 먼저 밝힙니다.
MLE
Maximum Likelihood Estimation
> 모델 파라메터를 observation 에만 의존하여 estimation
예시
모델: Probability density function f
모델의파라메터: θ
Observation: X = (x1, x2, …, xn)
n: 데이터개수
Likelihood
목표: θ값을estimation
방법: Likelihood 를 최대화
Estimation 수식
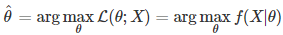
각데이터가서로 independent and identical distributed (id)하다는가정하에,
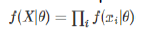
Log는 단조증가 함수 인데다가 곱셈을 덧셈으로 바꿔주므로,
계산의 편의를 위해, Log-likelihood 가 자주 이용됨
마무리는 Estimation 수식에 대한‘ 편미분‘
우리는 일반적으로 동전 하나를 던졌을 때 앞 또는
뒤가 나올 확률은 같다고 가정하여 0.5라고 생각한다.
하지만 이 0.5라는 확률 값은 정확한 값이 아니라 우리가 가정한 값이다.
때문에 몇 번 의 수행 결과로 동전의 앞면이 나올 확률 P(H)를 정하고자 한다.
만약 100번의 동전던지기를 수행했을 때, 앞면이 56번 나왔다면
‘동전을 던졌을 때 앞면이 나올 확률’은 얼마라고 얘기 할 수 있을까?
이 문제에 대한 해답을 구하는 것이 Maximum Likelihood Estimation 이다.
좀 더 자세하게 설명하면 앞에서 언급한 용어 L(T|E)에서,
증거 E는 앞면이 56 번 나왔다는 사실 이고, 이론 T를 변화시키면서
어느 이론이 가장 그 확률이 높은지 찾는 과정이다.
L(T|E)는 P(E|T) 를 최대화 하는 과정이기 때문에
이론 T가 ‘P(H) = 0.5’ 일 때를 계산하면 다음과 같다.
L[ P(X=56) ] =
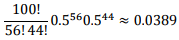
이와 같은 방법으로 몇몇 이론 T에 대해 값을 구해보면 다음 표와 같다.
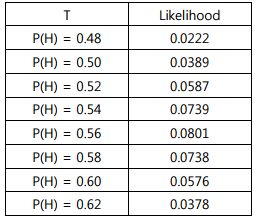
가정 T의 변화에 따른 Likelihood 의 변화
위 표에서 가장 높은 Likelihood를 가지는 이론 T는 P=0.56 일 때이다.
때문에 우리는 동전의 앞 면이 나올 확률이 0.5 라는 것을
전혀 모르는 상황에서 위와 같은 증거가 있을 때에는,
“동전을 던져서 앞면이 나올 확률은 0.56 이다” 라고 말할 수 있다.
이렇게 P(H)에 대한 확률을 모르는데,
어떠한 데이터가 주어진 경우,
이 데이터를 통해서 확률 P(H)를 추정하는 과정을
Maximum Likelihood Estimation 이라 한다.
Maximum Likelihood Estimation 예제-계속
Likelihood 수식(Binomial distribution)
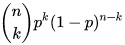
Log-likelihood 수식
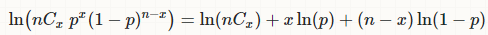
'미분= 0’ 으로전개
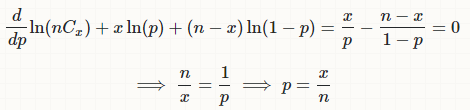
즉, MLE는Likelihood를통해cost를작게만들도록적용가능하다.
(log)Likelihood의‘음수’를최소화
MLE 단점
Observation 에전적으로의존하므로outlier 에민감
*outlier = 이상치
MAP
MLE 단점해결
> MLE는, 주어진 파라메터를 기반으로 데이터의 likelihood 를 최대화
> MAP 는, 주어진 데이터를 기반으로 최대 확률을갖는 파라메터 찾기
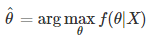
L: Likelihood 로서데이터로부터계산
f(θ): Prior probability 로서, parameter 자체의 확률 (사전지식이라 볼 수 있음)
Bayes Theorem 적용
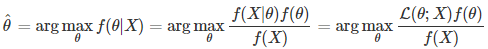
분자 부분에 대하여 비례하므로.. (또한, 데이터의iidassumption 적용)
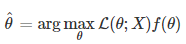
MAP 수식안에 Likelihood 가는데
즉 P(parameter) 만 알면 MLE 대신
MAP 사용이 가능한것을 의미한다.
예시
가정: 10만명에 대하여성 적분포(100점만점)를 구할때,
10명만 샘플링하여 parameter estimation 을 수행 하려고함
10명이약70점을평균값으로뭉쳐있는데,사실..
대부분의 데이터가‘80점’정도를 중심으로
Gaussian 을이룬다는 ‘경험‘(지식)을 가지고 있다면?
MLE 는10명분의 데이터에만 의존하므로, 70점 근처로 결과얻음
MAP 는’80점‘ 근처라는prior knowledge
를적용하여, 대략70~80점근처로결과얻음
데이터 자체만 의존하는게 아니라
사전 지식을 바탕으로 적용.
MLE가 가진 단점인 쓰레기 데이터를 고려 할 수 있다는 점을
f(θ): Prior probability 로서 단점을 해결할 수 있다.
즉 사전 지식의 무게를 줌으로써 outlier를 무시 해줄 수 있다.
언제 MLE, MAP를 쓸지 잘 분별하자.
하지만, 데이터 양이 충분히 많아지면,
Prior 값의 영향이 거의 없어진다는 연구 결과가 있음
> 데이터가 너무 방대하면 사전지식에 대한 기준이 약해진다!!
즉 데이터의 양이 작고 우리가 사전지식에 의존한다면 - > MAP
'Big Data > ML' 카테고리의 다른 글
| Bayesian network. (0) | 2019.04.10 |
|---|---|
| Decision Tree (0) | 2019.04.10 |
| PCA SVD, Linear Discriminant Analysis (0) | 2019.04.08 |
| Machine Learning - Feature 와 Model. (0) | 2019.04.05 |
| Evaluation (0) | 2019.04.05 |




