nathan_H
PCA SVD, Linear Discriminant Analysis 본문
참고 블로그 - https://darkpgmr.tistory.com/106
- https://ratsgo.github.io/from%20frequency%20to%20semantics/2017/04/06/pcasvdlsa/
기저
벡터 공간 V에 대하여
임의의 벡터 집합 S가 서로 '1차 독립'
이면서 V를 '생성'하면 S를 V의 기저라고 한다.
1차 독립(선형 독립)
서로가 선형의 곱으로 표현 x
2-dimensional 좌표계(x, y 축)
V1 = (1, 0)
V2 = (0, 1)
V1과 V2는 서로 1차 독립이면서
좌표계의 모든 벡터를 1차 결합을 통해 표현 가능.
3D좌표계의 기저는?
-> x, y, z축
고유값, 고유벡터
고유벡터
-> 선형 변화 A에 의한 변환 결과가 자기 자신의
상수배가 되는 0이 아닌벡터
고유값
-> 고유벡터에서의 상수배.
*행렬 곱의 의미
-> 변화(확대 / 축소 / 회전)
SVD
Singular Value Decomposition
-> M X N 크기의 행렬 A에 대하여,
3개의 행렬의 내적으로 나타낼 수 있다.
A=UΣVT

행렬 U와 V에 속한 열벡터는 특이벡터(singular vector)로 불리고요,
모든 특이벡터는 서로 직교하는 성질을 지닙니다.
행렬 Σ의 특이값은 모두 0보다 크거나 같으며 내림차순으로 정렬돼 있습니다.
행렬 Σ의 k번째 대각원소에 해당하는 Σk는
행렬 A의 k번째 고유값에 제곱근을 취한 값과 같습니다.
따라서 식 (1), A = UΣVT에서 U, V는 직교행렬, Σ는 대각행렬이므로
Ax는 x를 먼저 VT에 의해 회전시킨 후 Σ로 스케일을 변화시키고 다시 U로 회전시키는 것임을 알 수 있다.

<그림1> 출처: 위키피디아
즉, 행렬의 특이값(singular value)이란 이 행렬로 표현되는
선형변환의 스케일 변환을 나타내는 값으로 해석할 수 있다.
고유값분해(eigendecomposition)에서 나오는 고유값(eigenvalue)과
비교해 보면 고유값은 변환에 의해 불변인 방향벡터(-> 고유벡터)에 대한 스케일 factor이고,
특이값은 변환 자체의 스케일 factor로 볼 수 있다.
PCA 분석
Principal Component Analysis
주성분 분석(PCA, Principal Component Analysis)은 가장 대표적인 차원 축소 알고리즘이다.
PCA는 먼저 데이터에 가장 가까운 초평면(hyperplane)을 구한 다음,
데이터를 이 초평면에 투영(projection)시킨다.
데이터의 분포에 대한 주성분을 찾는 것
-> 데이터의 패턴을 잘 표현해주는 최적의 feature 조합을 찾는 것!
즉 feature selection 과 feature dimension reduction을 위해 쓰인다.
분산 보존
저차원의 초평면에 데이터를 투영하기 전에
먼저 적절한 초평면을 선택해야 한다.
PCA는 데이터의 분산이 최대가 되는 축을 찾는다.
즉, 원본 데이터셋과 투영된 데이터셋 간의 평균제곱거리를 최소화 하는 축을 찾는다.
아래의 그림에서 왼쪽 2차원 데이터셋을 오른쪽 그림처럼 투영했을 때 축
으로 투영한 데이터가 분산이 최대로 보존되는 것을 확인할 수 있다.

PCA는 다음과 같은 단계로 이루어진다.
-
학습 데이터셋에서 분산이 최대(longest distance)인 축(axis)을 찾는다.
-
이렇게 찾은 첫번째 축과 직교(orthogonal)하면서 분산이 최대인 두 번째 축을 찾는다.
-
첫 번째 축과 두 번째 축에 직교하고 분산을 최대한 보존하는 세 번째 축을 찾는다.
-
1~3과 같은 방법으로 데이터셋의 차원(특성 수)만큼의 축을 찾는다.
출처: https://excelsior-cjh.tistory.com/167 [EXCELSIOR]

이렇게 -번째 축을 정의하는 단위 벡터(unit vector)를 -번째
주성분(PC, Principal Component)이라고 한다.
예를들어, 위의 그림에서는 2차원 데이터셋이므로
PCA는 분산을 최대로 보존하는 단위벡터 이 구성하는 축과
이 축에 직교하는 가 구성하는 축을 찾게 된다.
출처: https://excelsior-cjh.tistory.com/167 [EXCELSIOR]
구하는 방법
1) 데이터들의 평균으로 원점을 가정
2) 데이터들에 대한 공분산 행렬, 고유값, 고유벡터 구함
3) 고유벡터 기반으로 데이터를 보면, 가장 큰 분산을 가지게 됨
분산을 최대로 주는 eigen vector를 찾는 것이니
Feature가 m개일 경우, 공분산 행렬은
m x m 크기의 행렬이 됨
즉 서로 '연관'있는 feature pair들을 파악할 수 있게 된다.
> 이에 대한 고유값, 고유벡터를 얻는 것은,
결국 correlation 존재하는 feature들에 대한
기저를 확보하는 작업.
> 즉 공분산 행렬을 통해
상호관계가 존재하는 feauture들에 기저를 확보하는 것이다.
고유벡터를 기저라고 가정하고 데이터를 보게 되면,
correlation 이 컸던 feature pair 들의 관점에서 보게 되므로,
분산이 커진다.
PCA의 목적은 원데이터 행렬 X의 분산을 최대한 보존하는 데
Z의 분산 또한 최대화을 해야 한다.

그럼 우리가 알고 싶은 미지수인 p차원 계수벡터를 α,
X의 공분산행렬(covariance matrix)을 Σ로 둡시다.
그럼 아래와 같이 식을 쓸 수 있습니다.
maxα{Var(Z)}
=maxα{Var(α→TX)}
=maxα{α→TVar(X)α→}
=maxα{α→TΣα→}
PCA 정리
1) 공분산이 매우 중요한 척도 이므로 "분산"이 작은 것을 중요하게 여기는 데이터에는 부적합
2) 데이터들의 분산이 직교하지 않는 경우에 부적합.
3) 데이터 feature dimension 이 큰 경우, PCA등 과 같은 방법으로
Feature dimesion을 줄여줘 도움을 줄수 있다
4) PCA, SVD는 모두 classifier 가 아니다.
Linear Discriminant Analysis
선형 판별 분석
> 클래스간 분산과 클래스 내 분산의 비율을 최대화 하는 방식으로 feature dimesion 축소
> 임의의 벡터에 projection 했을때 클래스들의 판별을 더 잘할 수 있게 해준다.
projection 참고 블로그.
*https://ratsgo.github.io/linear%20algebra/2017/10/20/projection/
사영(projection) · ratsgo's blog
이번 글에서는 머신러닝의 다양한 분야에서 폭넓게 응용되고 있는 선형대수학의 기본 개념인 사영(projection)에 대해 살펴보도록 하겠습니다. 이 글은 고려대 강필성 교수님, 역시 같은 대학의 김성범, 한성원 교수님 강의와 위키피디아 등의 자료를 제 나름대로 정리했음을 먼저 밝힙니다. 그럼 시작하겠습니다. 벡터의 내적과 사영 벡터 $b$를 벡터 $a$에 사영한 결과($x$)는 아래 그림과 같습니다. 벡터 덧셈의 기하학적 성질을 이용해 위 그림에서 정보를
ratsgo.github.io
*PCA와 달리 class 까지 고려하여 찾음
LDA 도 결국은 Classifier 가 아니다.
찾고자하는 벡터w에 클래스의 중심을 projection 했을때,
그 거리를 최대화 해야 함


Projection 된중심들

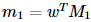
최대화 해야 할 목적함수

분자 전개(data: d x 1, SB: d x d, m: d x d)
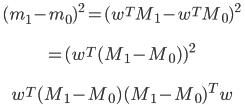
𝑆𝐵=(𝑀1−𝑀0)(𝑀1−𝑀0)T
분모 전개(SW: d x d )



수식(두개의클래스C0, C1가있다고가정)
목적함수간략화버전

𝑆𝐵=(𝑀1−𝑀0)(𝑀1−𝑀0)T
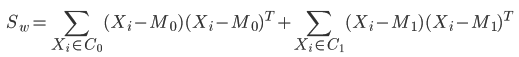

LDA 용도
> 클래스 간의 분류가 용이한 다른 feature 축으로 변환 /축소
> 본질은 classifier는 아니지만 분류에 적용 가능
한계
> 각 클래스의 중심에 데이터가 몰려 있다는 가정을 두고 있으므로
비선형으로 분포된 데이터에는 부적적하다.
PCA LDA 비교.

'Big Data > ML' 카테고리의 다른 글
| Bayesian network. (0) | 2019.04.10 |
|---|---|
| Decision Tree (0) | 2019.04.10 |
| MLE, MAP (0) | 2019.04.09 |
| Machine Learning - Feature 와 Model. (0) | 2019.04.05 |
| Evaluation (0) | 2019.04.05 |




